La Función Gamma de Euler y
el factorial
Adrian María Legendre (1752-1833) propuso, en 1814, llamar Función
Gamma y representar con la letra correspondiente, G, a
una función que había sido introducida por primera vez en una carta que
escribió Leonard Euler (1707-1783) a Christian Goldbach (1690-1764) en el año
1729. Esta función fue descrita inicialmente en forma infinitesimal, como el
límite de una expresión discreta. Más tarde se obtuvieron expresiones
integrales. La primera de estas integrales fue ya deducida por el mismo Euler,
y era:
Ésta es
una integral impropia que no puede calcularse en términos de funciones
elementales.
¿Cuál
es su relación con el factorial de un número?
Veamos,
lo primero que tenemos que hacer es realizar la integración por partes de la
función gamma. Para ello tomaremos:
, de donde derivando tenemos: 
y 
, de donde integrando
tenemos: 
y, utilizando la expresión de la
integración por partes: 
, obtenemos:
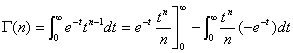
en esta expresión, utilizando la
regla de Barrow, según la cual 
y utilizando un
límite cuando t tiende a infinito para evaluar el extremo impropio, podemos
calcular el primer sumando:
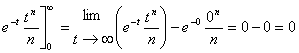
Nos queda, entonces:
es decir, hemos obtenido:
de donde:
si reiteramos esta relación
obtenemos:
generalizando, hemos obtenido:
De esta forma, 0! es el valor de G(0+1), es decir, el valor de G(1).
Para saber los valores de la
función gamma hay que recurrir a tablas, o a su gráfica, que es:
donde podemos ver que el valor correspondiente es 1, es decir:
0! = 1
Bibliografía.-
1.- http://personales.ya.com/casanchi/mat/funciongamma01.htm