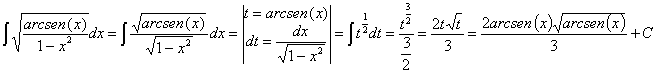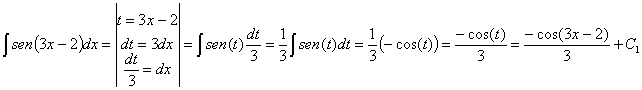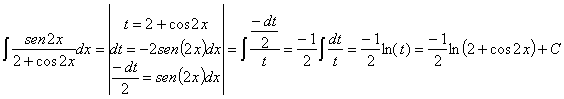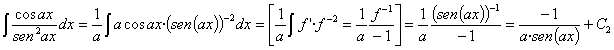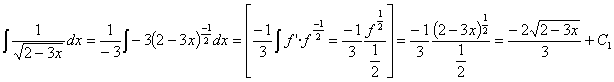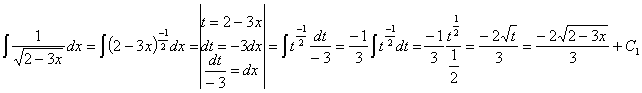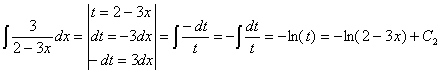Presta especial atención a las integrales número 47, 48, 49 y 50
1) ![]() *
*
RESOLUCIÓN: utilizando la relación fundamental de la trigonometría esta integral se convierte en otra que es inmediata: 1 – sen2x = cos2x
![]()
RESOLUCIÓN: esta es la integral de una función potencial y, por lo tanto, es inmediata.
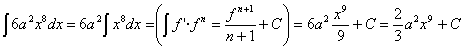
3) ![]()
RESOLUCIÓN: esta es la integral la podemos separar en sumas y restas de funciones potenciales y, por lo tanto, es inmediata.
![]()
simplificando: ![]()
4) ![]()
RESOLUCIÓN: esta integral es inmediata como función potencial expresando la raíz como una potencia.
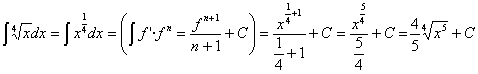
5) ![]()
RESOLUCIÓN: esta integral se puede separar en sumas y restas de funciones potenciales (expresando las raíces como potencias) y, por lo tanto, es inmediata.
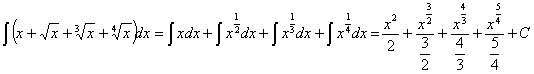
operando, expresando las potencias como raíces y simplificándolas obtenemos:
![]()
6) ![]()
RESOLUCIÓN: esta integral se puede separar en sumas y restas de funciones potenciales (expresando las raíces como potencias) y, por lo tanto, es inmediata.
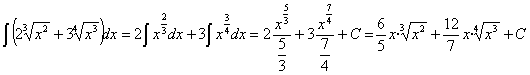
7) 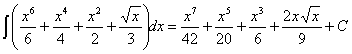
RESOLUCIÓN: esta integral se puede separar en sumas y restas de funciones potenciales (expresando la raíz como potencia) y, por lo tanto, es inmediata.
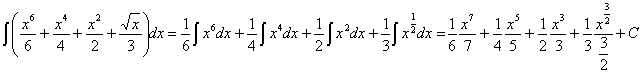
operando, expresando las potencias como raíces y simplificándolas obtenemos:
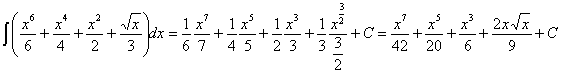
8) 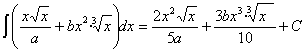 , siendo “a” y “b” constantes
, siendo “a” y “b” constantes
RESOLUCIÓN: esta integral se puede separar en sumas y restas de funciones potenciales (expresando las raíces como potencias y agrupando) y, por lo tanto, es inmediata.
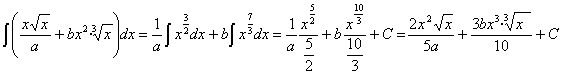
operando, expresando las potencias como raíces y simplificándolas obtenemos:
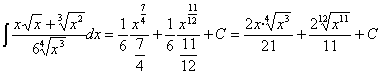
10) ![]()
RESOLUCIÓN: separamos la integral en suma de integrales y aplicamos
las siguientes reglas de integración: ![]() y
y ![]()
![]()
RESOLUCIÓN: separamos la integral en suma de integrales y expresamos las raíces como potencias.
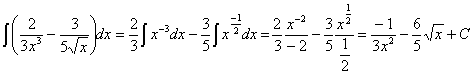
12) ![]()
RESOLUCIÓN: separamos la integral en suma de integrales y aplicamos
las siguientes reglas de integración: ![]() y
y ![]()
![]()
13) ![]() , siendo “a” una constante
, siendo “a” una constante
RESOLUCIÓN: separamos la integral en suma de integrales y aplicamos
las siguientes reglas de integración: ![]() ,
, ![]() y
y ![]()
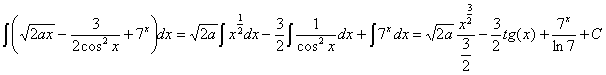
operando, expresando las potencias como raíces y simplificándolas obtenemos:
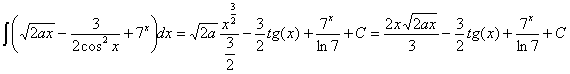
RESOLUCIÓN: separamos la integral en resta de integrales y
aplicamos las siguientes reglas de integración: ![]() y
y ![]()
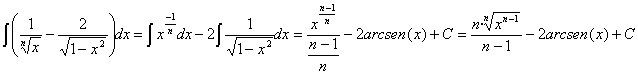
15) ![]()
RESOLUCIÓN: NO podemos separar la integral del producto en producto de integrales... así que lo mejor que podemos hacer es desarrollar el producto y separar después la integral en sumas de integrales.
![]()
ahora evaluamos cada una de las integrales:
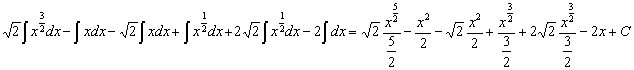
agrupamos, simplificamos y expresamos las potencias como raíces y queda:
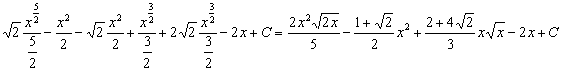
16) 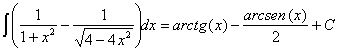
RESOLUCIÓN: separamos la integral en resta de integrales y
aplicamos las siguientes reglas de integración: ![]() y
y ![]() . Para poder aplicar la segunda de las leyes deberemos
extraer de la integral las constantes que ocultan la forma de la función
. Para poder aplicar la segunda de las leyes deberemos
extraer de la integral las constantes que ocultan la forma de la función
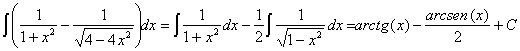
17) 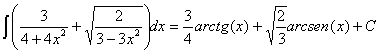
RESOLUCIÓN: separamos la integral en suma de integrales y aplicamos
las siguientes reglas de integración: ![]() y
y ![]() . Para poder aplicar estas reglas deberemos extraer de la
integral las constantes que ocultan la forma de la función.
. Para poder aplicar estas reglas deberemos extraer de la
integral las constantes que ocultan la forma de la función.
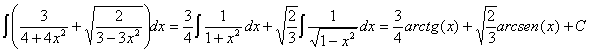
18) 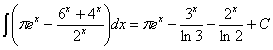
RESOLUCIÓN: separamos la integral en resta de integrales y
aplicamos las siguientes reglas de integración: ![]() y
y ![]() . Para poder aplicar la segunda regla debemos separar el
quebrado en dos y simplificar las potencias.
. Para poder aplicar la segunda regla debemos separar el
quebrado en dos y simplificar las potencias.
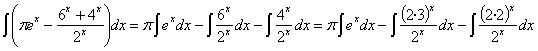
aplicamos la potencia del producto y simplificamos:
![]()
ahora aplicamos las reglas de integración:
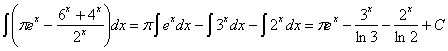
19) ![]()
RESOLUCIÓN: separamos la integral en resta de integrales y
aplicamos las siguientes reglas de integración: ![]() ,
, ![]() y
y![]()
![]()
La primera de las integrales la
resolveremos por partes: ![]() . La segunda es inmediata:
. La segunda es inmediata:
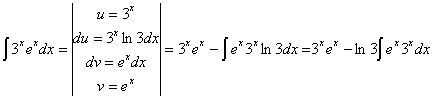
como obtenemos de nuevo la integral inicial despejamos su valor:
![]()
de donde:
![]()
y la segunda integral, que es inmediata, da:
![]()
Agrupando los resultados obtenidos:
![]()
queda:
![]()
20) 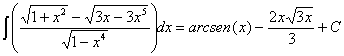
RESOLUCIÓN: separamos la integral en resta de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas.
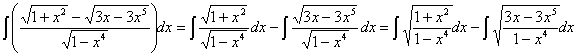
factorizando y simplificando:
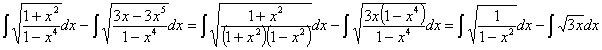
ahora ya tememos integrales
inmediatas para las que utilizaremos las reglas de integración ![]() y
y ![]() :
:
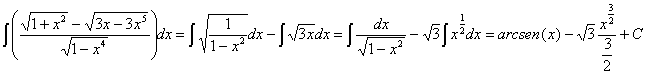
queda:
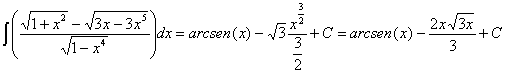
21) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
potencial que se puede integrar utilizando la regla de integración ![]() :
:
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
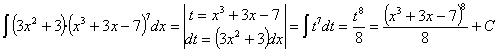
22) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
racional que se puede integrar utilizando la regla de integración ![]() :
:
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
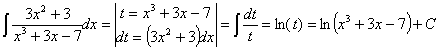
23) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
potencial que se puede integrar utilizando la regla de integración ![]() , basta con expresar la raíz como potencia:
, basta con expresar la raíz como potencia:
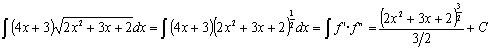
operando, expresando las potencias como raíces y simplificándolas obtenemos:
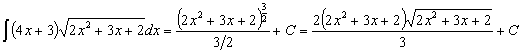
Esta integral también se puede
resolver haciendo un cambio de variable llamando t a la función: 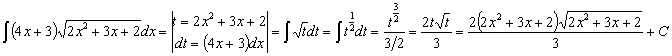
24) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
potencial que se puede integrar utilizando la regla de integración ![]() :
:
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
![]()
25) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
potencial que se puede integrar utilizando la regla de integración ![]() . Para ello expresamos la raíz como potencia y observamos que
casi tenemos la derivada de la base de la potencia (basta con añadir, y quitar,
un signo menos al seno):
. Para ello expresamos la raíz como potencia y observamos que
casi tenemos la derivada de la base de la potencia (basta con añadir, y quitar,
un signo menos al seno):
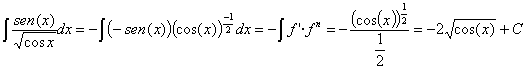
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
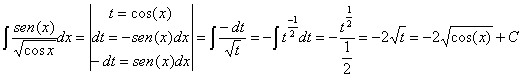
26) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
exponencial en la que tenemos la derivada del exponente. Por lo tanto podemos
utilizar la regla de integración ![]() .
.
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
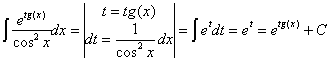
27) ![]()
RESOLUCIÓN: esta integral es inmediata. Para verlo hay que expresar
la tangente como seno entre coseno. Entonces vemos que se trata de una función
racional en la que casi tenemos como numerador la derivada del denominador
(basta con poner, y quitar, un signo menos). Por lo tanto podemos utilizar la
regla de integración ![]() .
.
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
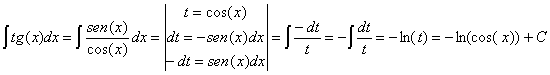
28) ![]()
RESOLUCIÓN: esta integral es inmediata. Para verlo hay que expresar
la cotangente como coseno entre seno. Entonces vemos que se trata de una
función racional en la que tenemos como numerador la derivada del denominador.
Por lo tanto podemos utilizar la regla de integración ![]() .
.
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
![]()
29) ![]()
RESOLUCIÓN: esta
integral es casi inmediata. Se trata de un arcotangente: ![]() , pero necesitamos la derivada del coseno, que es el menos
seno. Por ello pondremos (y quitaremos) un signo menos:
, pero necesitamos la derivada del coseno, que es el menos
seno. Por ello pondremos (y quitaremos) un signo menos:
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
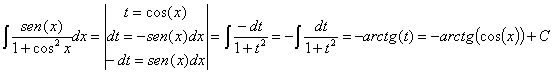
30) ![]()
RESOLUCIÓN: esta
integral es inmediata. Se trata de una función potencial donde tenemos la
derivada de la base. Utilizaremos la regla de integración ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
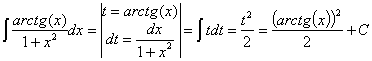
31) ![]()
RESOLUCIÓN: esta
integral es inmediata. Se trata de una función tipo arcotangente donde
tenemos la derivada de la función. Utilizaremos la regla de integración ![]()
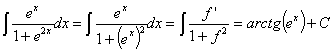
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
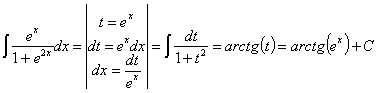
32) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función tipo
arcoseno donde casi tenemos la derivada de la función (basta con añadir y
quitar el ln2). Utilizaremos la regla de integración ![]()
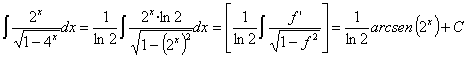
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
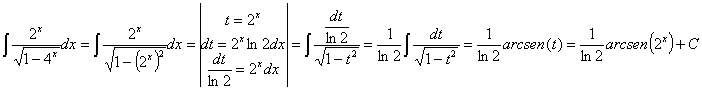
33) ![]()
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
racional en la que casi tenemos como numerador la derivada del denominador
(basta con multiplicar, y dividir, por 2). Por lo tanto podemos utilizar la
regla de integración ![]() .
.
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
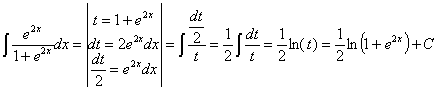
34) ![]()
RESOLUCIÓN: separamos el quebrado en dos y la integral resultante en resta de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas.
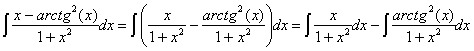
Vamos a resolver cada una de las nuevas integrales por separado.
La primera de ellas es una
racional donde casi tenemos en el numerador la derivada del denominador (basta
con multiplicar y dividir por 2). Podemos utilizar la regla de integración ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
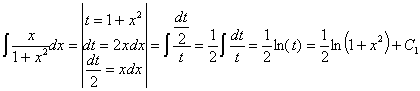
La segunda de las integrales es
una potencial (arcotangente al cuadrado) donde tenemos la derivada de la base.
Por lo tanto es inmediata utilizando la regla de integración ![]()
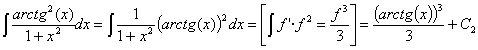
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
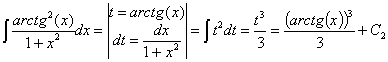
Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
![]()
35) ![]()
RESOLUCIÓN: Esta integral es una potencial (arcoseno elevado a ½ donde
tenemos la derivada de la base. Por lo tanto es inmediata utilizando la regla
de integración ![]()
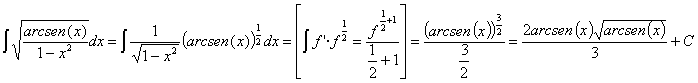 Esta integral también se puede resolver haciendo un cambio de
variable llamando t a la función f:
Esta integral también se puede resolver haciendo un cambio de
variable llamando t a la función f:
36) ![]()
RESOLUCIÓN: Esta integral es una exponencial donde casi tenemos la
derivada del exponente (la derivada de la raíz de x es uno partido por dos
veces la raíz: ![]() , así que multiplicamos y dividimos por 2). Podemos utilizar
la regla de integración
, así que multiplicamos y dividimos por 2). Podemos utilizar
la regla de integración ![]()
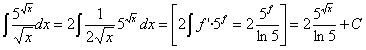
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
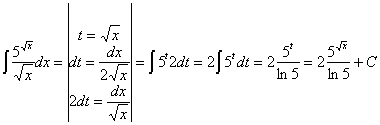
37) ![]()
RESOLUCIÓN: Esta integral es una racional donde tenemos la derivada
del denominador. Podemos utilizar la siguiente regla de integración: ![]()
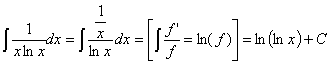
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
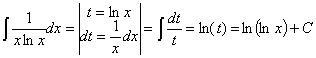
38) ![]()
RESOLUCIÓN: separamos el quebrado en dos y la integral resultante en resta de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas.
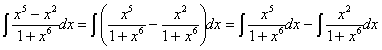
Vamos a resolver cada una de las nuevas integrales por separado.
La primera de ellas es una
racional donde casi tenemos en el numerador la derivada del denominador (basta
con multiplicar y dividir por 6). Podemos utilizar la regla de integración ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
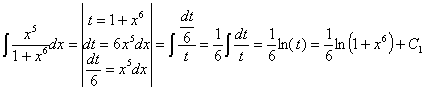
La segunda de las integrales es
del “tipo arcotangente”. Para verlo basta con expresar x6 como un
cuadrado (x3)2. Por lo tanto es inmediata utilizando la
regla de integración ![]() y completando la
derivada de f (para esto multiplicamos y dividimos por 3):
y completando la
derivada de f (para esto multiplicamos y dividimos por 3):
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
![]()
39) 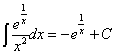
RESOLUCIÓN: esta integral es inmediata. Se trata de una función
exponencial en la que casi tenemos la derivada del exponente: ![]() , bastaría con multiplicar por –1. Por lo tanto podemos
utilizar la regla de integración
, bastaría con multiplicar por –1. Por lo tanto podemos
utilizar la regla de integración ![]() .
.
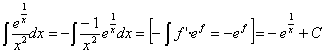
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
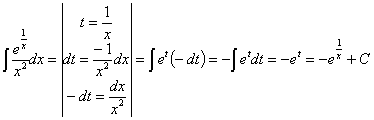
40) ![]()
RESOLUCIÓN: Esta integral es una potencial (un polinomio elevado a
1/7 donde casi tenemos la derivada de la base (basta con multiplicar y dividir
por –4). Por lo tanto es inmediata utilizando la regla de integración ![]()
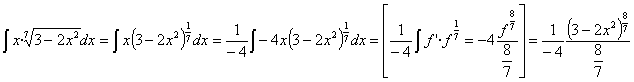
operando y simplificando obtenemos:
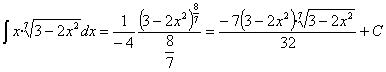
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
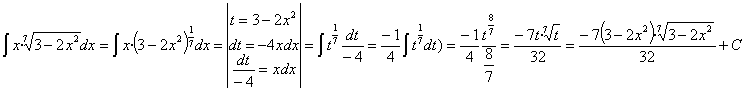
41) 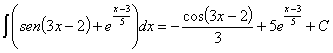
RESOLUCIÓN: separamos la integral en suma de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas.
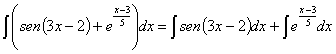
Vamos a resolver cada una de las nuevas integrales por separado.
La primera de ellas es inmediata,
ya que la derivada del argumento del seno es una constante. Vamos a utilizar la
regla de integración ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
La segunda integral es inmediata.
Se trata de una función exponencial en la que casi tenemos la derivada del
exponente: ![]() , bastaría con multiplicar y dividir por 1/5. Por lo tanto
podemos utilizar la regla de integración
, bastaría con multiplicar y dividir por 1/5. Por lo tanto
podemos utilizar la regla de integración ![]() .
.
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
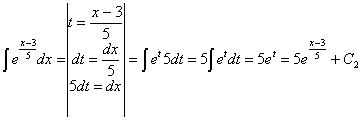
Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
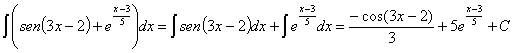
42) 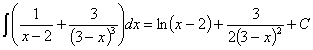
RESOLUCIÓN: separamos la integral en suma de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas
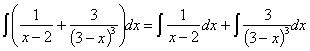
Vamos a resolver cada una de las nuevas integrales por separado.
La primera de ellas es una
racional donde tenemos en el numerador la derivada del denominador. Podemos
utilizar la regla de integración ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
![]()
La segunda de las integrales es
una potencial (3-x elevado a –3) donde casi tenemos la derivada de la base
(basta con multiplicar por –1 y extraer el 3 como constante que es). Por lo
tanto es inmediata utilizando la regla de integración ![]()
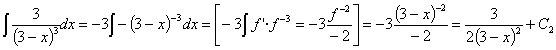
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
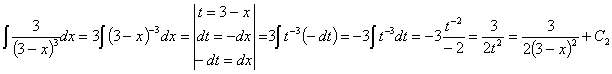
Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
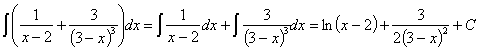
43) ![]()
RESOLUCIÓN: separamos la integral en resta de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas
![]()
Vamos a resolver cada una de las nuevas integrales por separado.
La primera de ellas es una
exponencial donde casi tenemos la derivada del exponente (la derivada 7x – 2 es
7, así que multiplicamos y dividimos por 7). Podemos utilizar la regla de
integración ![]()
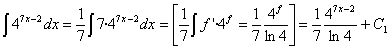
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
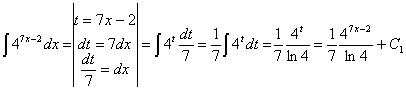
La segunda de las integrales es una trigonométrica
inmediata. Únicamente falta la derivada del argumento del coseno, que es 2. Por
ello multiplicamos y dividimos por 2 y aplicamos la regla de integración ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
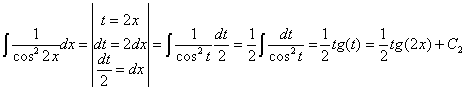
Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
![]()
44) ![]()
RESOLUCIÓN: Esta integral es una racional donde casi tenemos la
derivada del denominador. La dreivada de 2+cos2x es –2sen2x, así que basta con
multiplicar y dividir por –2. Podemos utilizar la siguiente regla de
integración: ![]()
![]()
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
45) ![]() , siendo “a” una constante.
, siendo “a” una constante.
RESOLUCIÓN: separamos el quebrado en dos y la integral resultante en suma de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas.
![]()
Vamos a resolver cada una de las nuevas integrales por separado.
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
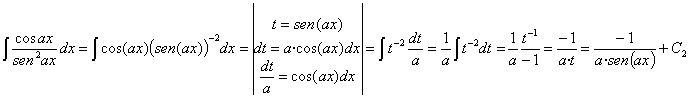 Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
Ahora sustituimos los resultados de las dos integrales y
consideramos C=C1+C2
![]()
46) 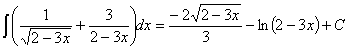
RESOLUCIÓN: separamos la integral en suma de integrales y tratamos de desarrollar las expresiones en cada una de ellas para ver si obtenemos integrales inmediatas
![]()
Vamos a resolver cada una de las nuevas integrales por separado.
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función f:
Ahora sustituimos los resultados de las dos integrales y consideramos C=C1+C2
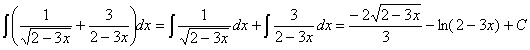
47) ![]()
RESOLUCIÓN: vamos a desarrollar el cuadrado para poder separar la integral en suma de integrales.
![]()
Ahora resolveremos cada una de las integrales por separado.
La integral del coseno cuadrado y la del seno cuadrado se desarrollan utilizando las relaciones del ángulo mitad. Las relacionamos de la siguiente manera:
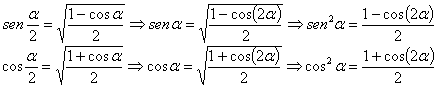
Así la primera integral se puede expresar:
![]()
Y la tercera integral se puede expresar:
![]()
![]()
Ahora sustituimos los resultados de las tres integrales y
consideramos C=C1+C2+C3
![]()
48) ![]()
RESOLUCIÓN: vamos a utilizar un cambio de variable no trivial. Trataremos de que desaparezca la raíz, así que tomaremos t2=x+3
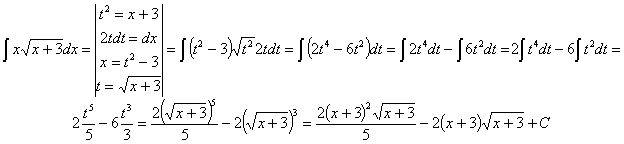
Lo que hemos conseguido con este cambio de variable es la integral de un polinomio que podemos separar en sumas y restas, todas de integración inmediata.
49) ![]()
RESOLUCIÓN: esta integral es similar a la anterior, por lo que seguiremos la misma estrategia. Haremos el cambio de variable t2=x–2 y desarrollaremos lo que salga: Después desharemos el cambio.
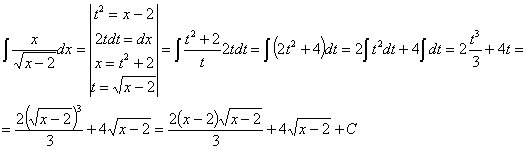
50) ![]()
RESOLUCIÓN: esta integral es similar a las dos anteriores, por lo que seguiremos la misma estrategia, es decir, trataremos de eliminar la raíz (cúbica en este caso). Haremos el cambio de variable t3=x+1 y desarrollaremos lo que salga: Después desharemos el cambio.
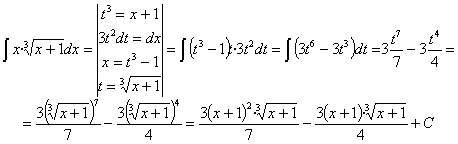
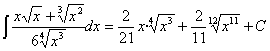
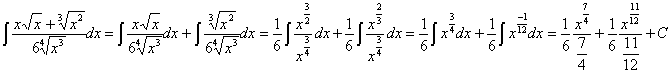
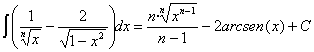 , siendo “n” una constante
, siendo “n” una constante