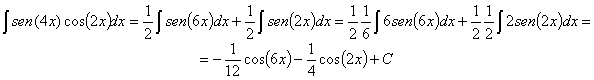Presta especial atención a las integrales número 60, 61, 65, 70, 73, 76, 79, 81, 87, 95 y 100.
51) 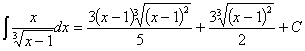
RESOLUCIÓN: esta integral es similar a las tres anteriores, por lo que seguiremos la misma estrategia, es decir, trataremos de eliminar la raíz (cúbica en este caso). Haremos el cambio de variable t3=x–1 y desarrollaremos lo que salga: Después desharemos el cambio.

52) ![]()
RESOLUCIÓN: esta es la integral de un
producto. Vamos a resolverla por partes: ![]()
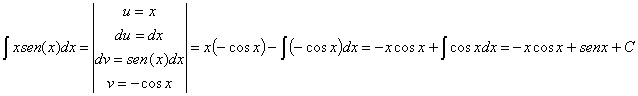
53) ![]()
RESOLUCIÓN: esta es la integral de un
producto. Vamos a resolverla por partes: ![]()
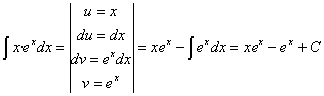
54) ![]()
RESOLUCIÓN: esta es la integral de un
producto. Vamos a resolverla por partes: ![]() Necesitaremos
reiterar el procedimiento:
Necesitaremos
reiterar el procedimiento:

vamos a reiterar el procedimiento eligiendo como función u, de nuevo, al polinomio. Esto lo hacemos así porque conforme derivemos u irá bajando el grado del polinomio hasta que desaparezca.
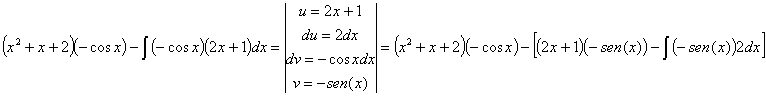
![]()
podemos agrupar el resultado obtenido agrupando los cosenos:
![]()
55) ![]()
RESOLUCIÓN: esta es la integral de un
producto. Vamos a resolverla por partes: ![]() Como función u
tomaremos el logaritmo. Esto lo hacemos así porque de lo contrario, si fuese
dv, habría que integrarlo, lo que no es sencillo.
Como función u
tomaremos el logaritmo. Esto lo hacemos así porque de lo contrario, si fuese
dv, habría que integrarlo, lo que no es sencillo.
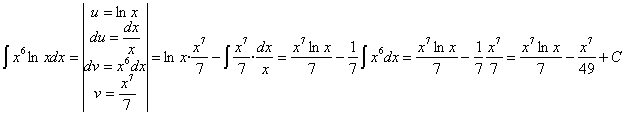
56) ![]()
RESOLUCIÓN: esta es la integral de un
producto. Vamos a resolverla por partes: ![]() Necesitaremos
reiterar el procedimiento:
Necesitaremos
reiterar el procedimiento:

vamos a reiterar el procedimiento. Hay que tener cuidado con los signos durante las operaciones:
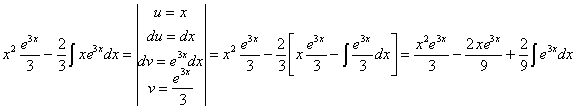
Ahora tenemos que integrar la exponencial, que es inmediata. Vamos a hacerla aparte y luego sustituiremos el resultado:
![]()
Sustituimos en la expresión antes hallada:
![]()
en este resultado podemos sacar factor común las exponenciales y agrupar el polinomio:
![]()
57) ![]()
RESOLUCIÓN: esta es la integral de un
producto. Vamos a resolverla por partes: ![]() Necesitaremos
reiterar el procedimiento eligiendo como función u, de nuevo, al polinomio.
Esto lo hacemos así porque conforme derivemos u irá bajando el grado del
polinomio hasta que desaparezca.
Necesitaremos
reiterar el procedimiento eligiendo como función u, de nuevo, al polinomio.
Esto lo hacemos así porque conforme derivemos u irá bajando el grado del
polinomio hasta que desaparezca.
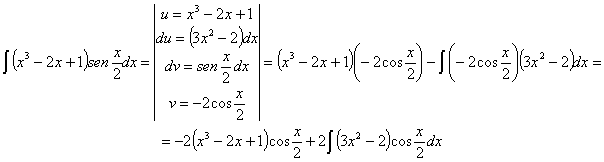
vamos a reiterar el procedimiento con la nueva integral que hemos obtenido. Luego sustituiremos lo hallado:
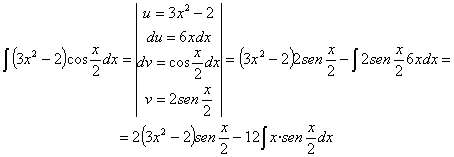
Sustituimos en el resultado anterior:
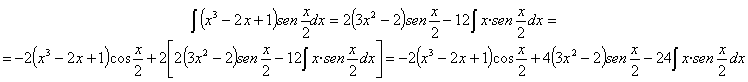
Por fin hemos llegado a una
integral inmediata. Basta con multiplicar y dividir por ½ para tener la
derivada del argumento del coseno. Aplicamos la regla de integración ![]()
![]()
Ya podemos sustituir el resultado encontrado en la cadena de integrales:
 Para expresar el resultado hemos agrupado en seno y coseno de
x/2.
Para expresar el resultado hemos agrupado en seno y coseno de
x/2.
58) ![]()
RESOLUCIÓN: esta integral se resuelve por partes (![]() ) de la siguiente manera:
) de la siguiente manera:
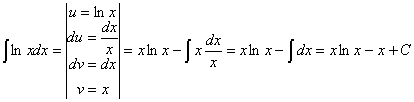
59) ![]()
RESOLUCIÓN: esta
integral se resuelve por partes (![]() ) de la siguiente manera:
) de la siguiente manera:
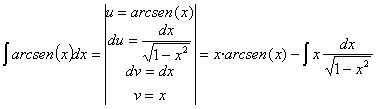
la nueva
integral que hemos obtenido es una potencial (polinomio 1-x2 elevado
a –1/2) donde casi tenemos la derivada de la base (basta con multiplicar y
dividir por –2). Utilizaremos para resolverla la regla de integración ![]()
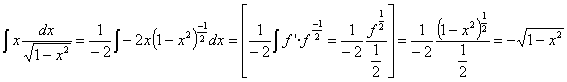
Ahora sustituimos el valor de la integral en el resultado hallado anteriormente:
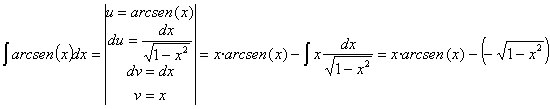
queda:
![]()
60) ![]()
RESOLUCIÓN: esta integral se resuelve
por partes (![]() ). Presenta la particularidad de que al reiterar el
procedimiento reaparece la integral inicial. Para terminar de resolverla hay
que agrupar las integrales.
). Presenta la particularidad de que al reiterar el
procedimiento reaparece la integral inicial. Para terminar de resolverla hay
que agrupar las integrales.
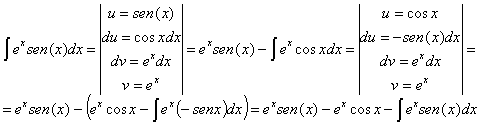
Como se puede ver después de reiterar el procedimiento vuelve a aparecer la integral inicial. Lo que haremos es despejar. De momento tenemos:
![]()
![]()
![]()
![]()
61) 
RESOLUCIÓN: esta es la integral de un producto. Vamos a resolverla
por partes: ![]() Necesitaremos
reiterar el procedimiento.
Necesitaremos
reiterar el procedimiento.
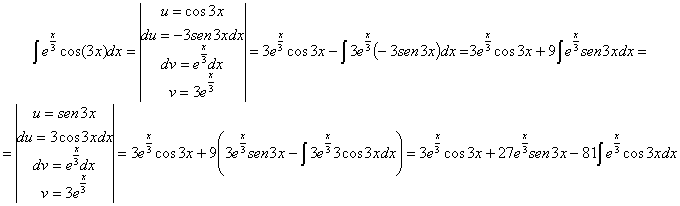 Como se puede ver
después de reiterar el procedimiento vuelve a aparecer la integral inicial. Lo
que haremos es despejar. De momento tenemos:
Como se puede ver
después de reiterar el procedimiento vuelve a aparecer la integral inicial. Lo
que haremos es despejar. De momento tenemos:
![]()
![]()
![]()
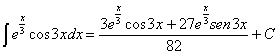
62) ![]()
RESOLUCIÓN: esta integral se puede resolver por partes. Como
función u tomaremos el polinomio, cuya derivación siempre simplifica el
polinomio. Como dv tomaremos la exponencial, que es fácil de integrar: ![]()
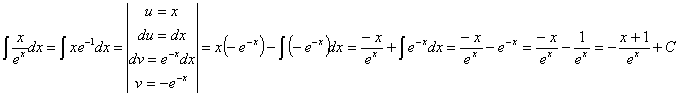
63) ![]()
RESOLUCIÓN: esta integral tiene un triple producto. Siempre que
tengamos el producto de un seno por un coseno podemos recurrir a la fórmula
trigonométrica del seno del ángulo doble: ![]() . Podemos recurrir a esta expresión multiplicando y
dividiendo por 2 en la integral:
. Podemos recurrir a esta expresión multiplicando y
dividiendo por 2 en la integral:
![]()
Ahora que tenemos la integral de un producto podemos
aplicar la integración por partes: ![]()
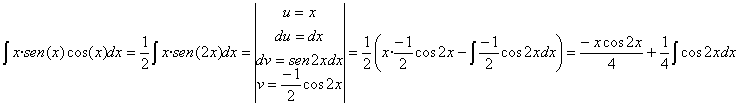
64) 
RESOLUCIÓN: podemos expresar esta integral como producto y utilizar
la integración por partes ![]() . Luego tomaremos como u el logaritmo, que es más fácil de
derivar que de integrar.
. Luego tomaremos como u el logaritmo, que es más fácil de
derivar que de integrar.
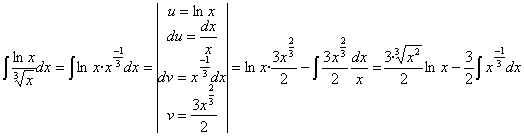
la integral que tenemos ahora es una inmediata de tipo potencial:
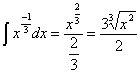
Ahora sustituimos el valor hallado:
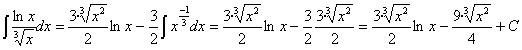
65) ![]()
RESOLUCIÓN: esta integral sería inmediata si el seno fuera de t en vez de ser el seno de un logaritmo. Por eso, como primer paso en la resolución vamos a hacer el cambio de variable t=lnx:
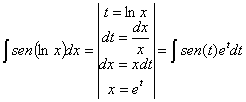
hemos necesitado expresar x en
función de t, y como t=ln(x) utilizando las leyes de los logaritmos x=et.
Ahora tenemos una integral, en función de t, que puede resolver por partes (de
hecho resolvimos la misma integral en el ejercicio 60, y daba![]() ). Sustituyendo el resultado obtenemos:
). Sustituyendo el resultado obtenemos:
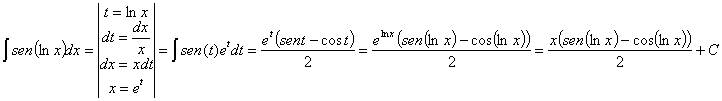
Para ver porqué elnx vale x hay que utilizar las leyes de los logaritmos: primero suponemos que elnx=k, y aplicamos logaritmos a la ecuación ln(elnx)=lnk. Ahora aplicamos las leyes de los logaritmos: lnx·lne=lnk, como lne=1 queda lnx=lnk, de donde x=k, es decir como supusimos que elnx=k, entonces elnx=x
66) ![]()
RESOLUCIÓN: esta integral es inmediata.
Se trata de una función racional que se puede integrar utilizando la regla de
integración ![]() :
:
![]()
Esta integral también se puede resolver haciendo un cambio de variable, llamando t a la función f:
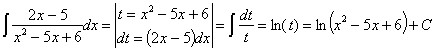
67) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x2–5x+6=(x–2)(x–3). Vamos a tratar de expresar el integrando como fracciones simples:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
![]()
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()
![]()
68) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x2–6x+8=(x–2)(x–4). Vamos a tratar de expresar el integrando como fracciones simples:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:

ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()
![]()
69) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x2–6x+8=(x–2)(x–4). Vamos a tratar de expresar el integrando como fracciones simples:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
![]()
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()
![]()
70) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Lo primero que podemos hacer es extraer de la integral las constantes que podamos:
![]()
Ahora factorizamos el denominador: x2–6x+9=(x–3)2 Tenemos una raíz repetida, por lo que vamos a expresar las fracciones simples de la siguiente manera:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
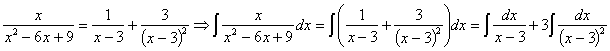
ahora tenemos dos integrales
inmediatas. La primera es una racional del tipo: ![]() , y la segunda es una potencial del tipo
, y la segunda es una potencial del tipo ![]() que debemos expresar
como (x–3)-2 para verla.
que debemos expresar
como (x–3)-2 para verla.
![]()
Ahora sustituimos este resultado en el primer desglose de la integral:
![]()
71) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar
resolver utilizando la técnica de fracciones simple. Ocurre que la
factorización no es exacta, pero eso no compromete la eficacia del método de
fracciones simples. Podemos factorizar utilizando la relación de diferencia de
cuadrados es igual al producto de suma por diferencia: ![]()
Ahora vamos a tratar de expresar el integrando como fracciones simples:
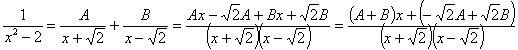
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
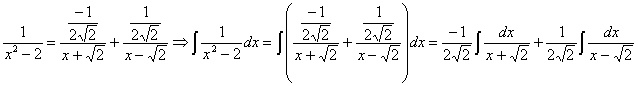
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()
![]()
y, racionalizando el resultado sale:
![]()
También podríamos utilizar propiedades de los logaritmos y expresar la solución así:

72) 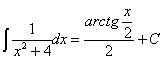
RESOLUCIÓN: esta integral se “parece” a la del arcotangente. Únicamente necesitamos que el 4 se convierta en 1. Esto podemos conseguirlo dividiendo numerador y denominador entre 4:

ahora tenemos una integral del
“tipo arcotangente”, que sería inmediata si dispusiéramos de la derivada de la
función, que es ½. Para ello multiplicamos y dividimos por ½ y aplicamos la
regla de integración ![]()
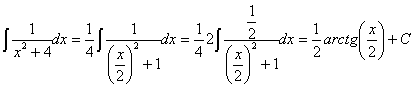
Esta integral también se puede resolver haciendo un cambio de variable llamando t a la función:
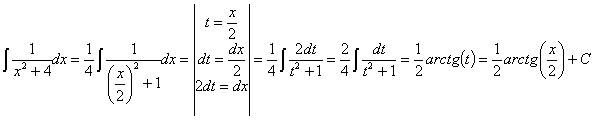
73) ![]()
RESOLUCIÓN: esta integral podría ser inmediata tipo racional si tuviéramos como numerador la derivada del denominador. Esto podemos conseguirlo manipulando el quebrado:
![]()
La primera de las integrales es una racional inmediata (es lo que hemos buscado).
![]()
Sustituimos:
![]()
74) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x2–6x–7=(x–7)(x+1). Vamos a tratar de expresar el integrando como fracciones simples:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
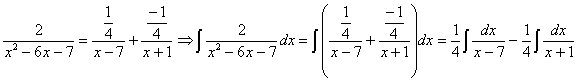
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()
![]()
podemos sacar factor común y aplicar las leyes de los logaritmos:
![]()
75) 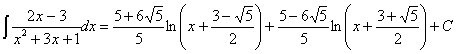
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simples. Nos vamos a encontrar con el problema de la factorización del denominador. Para encontrar las raíces del denominador lo igualamos a cero y resolvemos la ecuación de segundo grado:
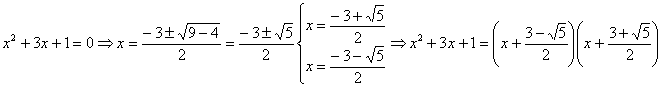
Vamos a tratar de expresar el integrando como fracciones simples:
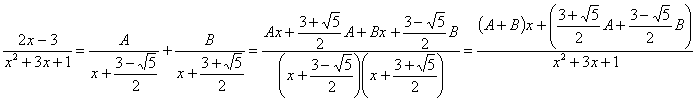
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
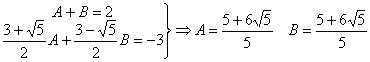
por lo tanto:
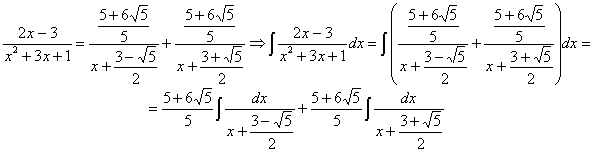
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()

76) ![]()
RESOLUCIÓN: esta integral podría ser inmediata tipo racional si tuviéramos como numerador la derivada del denominador. Esto podemos conseguirlo manipulando el quebrado:
![]()
La primera de las integrales es una racional inmediata al
tener como numerador la derivada del denominador. Podemos aplicar la regla de
integración ![]()
![]()
La segunda de las integrales se
puede manipular para convertirla en una potencial inmediata: ![]()
![]()
Sustituyendo queda:
![]()
Esta integral también puede hacerse por el método de fracciones simples, teniendo en cuenta que el denominador tiene raíces múltiples: x2-4x+4=(x–2)2 vamos a expresar las fracciones simples de la siguiente manera:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
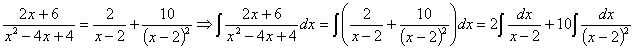
ahora tenemos dos integrales
inmediatas. La primera es una racional del tipo: ![]() , y la segunda es una potencial del tipo
, y la segunda es una potencial del tipo ![]() que debemos expresar
como (x–2)-2 para verla.
que debemos expresar
como (x–2)-2 para verla.
![]()
Hemos obtenido:
![]()
77) ![]()
RESOLUCIÓN: esta integral es una racional en la que casi tenemos
como numerador la derivada del denominador, bastaría con multiplicar y dividir
por 2. Podemos aplicar la regla de integración ![]()
![]()
También podemos resolver esta integral haciendo un cambio de variable, llamando t a la función:
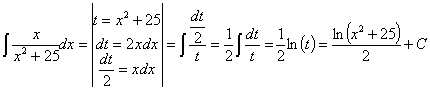
78) ![]()
RESOLUCIÓN: esta integral es una racional en la que el grado del numerador es mayor que el grado del denominador. Por ello lo primero es dividir los polinomios.
![]()
Sustituyendo en la integral:
![]()
Esta nueva integral la podemos resolver por la técnica de fracciones simples. Para ello hay que factorizar el denominador: (x2-9)=(x+3)(x–3). Vamos a tratar de expresar el integrando como fracciones simples:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
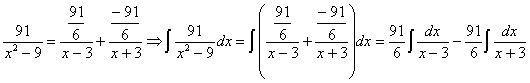
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]()
![]()
podemos sacar factor común y aplicar las leyes de los logaritmos:
![]()
Ahora podemos sustituir:
![]()
79) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x3+3x2–4x–12=(x+2)(x–2)(x+3). Vamos a tratar de expresar el integrando como fracciones simples:
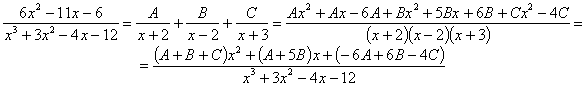
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
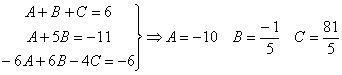
por lo tanto:
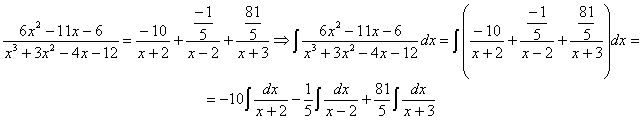
ahora tenemos tres integrales racionales inmediatas
utilizando la relación: ![]()
![]()
80) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x3–2x2–5x+6=(x+2)(x–3)(x–1). Vamos a tratar de expresar el integrando como fracciones simples:
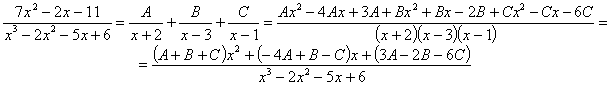
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
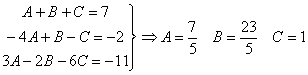
por lo tanto:

ahora tenemos tres integrales racionales inmediatas
utilizando la relación: ![]()
![]()
81) ![]()
RESOLUCIÓN: esta integral es una racional en la que el grado del numerador es mayor que el grado del denominador. Por ello lo primero es dividir los polinomios.
![]()
Sustituyendo en la integral:
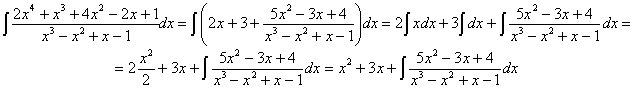
Esta nueva integral la podemos resolver por la técnica de fracciones simples. Para ello hay que factorizar el denominador: (x3–x2+x–1)=(x–1)(x2+1). Vamos a tratar de expresar el integrando como fracciones simples teniendo en cuenta que uno de los polinomios es de segundo grado:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
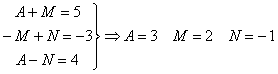
por lo tanto:
![]()
la primera de las integrales es una racional inmediata que
podemos resolver con: ![]()
![]()
En la segunda de las integrales podemos separar el quebrado y luego la integral en resta de integrales:
![]()
Ahora podemos sustituir todos estos resultados:
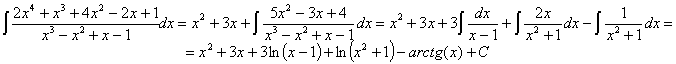
82) ![]()
RESOLUCIÓN: esta integral es una racional en la que casi tenemos
como numerador la derivada del denominador, bastaría con multiplicar y dividir
por 2. Podemos aplicar la regla de integración ![]()
![]()
También podemos resolver esta integral haciendo un cambio de variable, llamando t a la función:

83) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x3–5x2+6x=x(x–3)(x–2). Vamos a tratar de expresar el integrando como fracciones simples:

Comparando el numerador del quebrado inicial y el final planteamos el sistema:
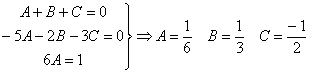
por lo tanto:
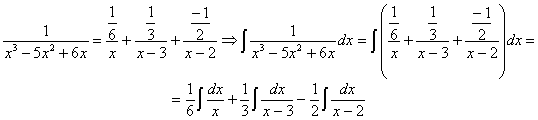
ahora tenemos tres integrales racionales inmediatas
utilizando la relación: ![]()
![]()
84) 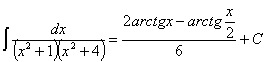
RESOLUCIÓN: esta es una integral racional que podemos intentar por fracciones simples. Si conseguimos separar los dos factores podemos tratar de encontrar integrales del tipo arcotangente. Por eso vamos a tratar de expresar el integrando como fracciones simples de la siguiente manera:
![]()
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
![]()
por lo tanto:
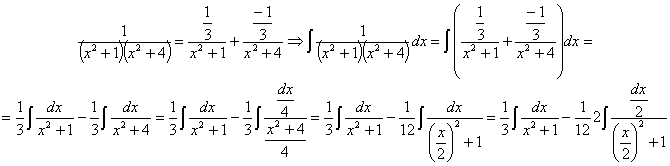
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]() Queda:
Queda:
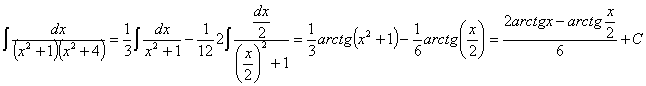
85) ![]()
RESOLUCIÓN: esta integral, como racional que es, se puede intentar resolver utilizando la técnica de fracciones simple. Para ello factorizamos el denominador: x3–5x2+4x=x(x–1)(x–4). Vamos a tratar de expresar el integrando como fracciones simples:
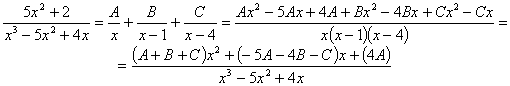
Comparando el numerador del quebrado inicial y el final planteamos el sistema:
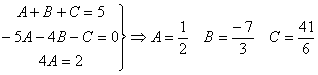
por lo tanto:
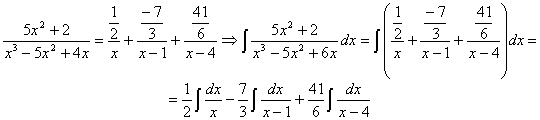
ahora tenemos tres integrales racionales inmediatas
utilizando la relación: ![]()
![]()
86) ![]()
RESOLUCIÓN: esta integral es una racional en la que el grado del numerador es mayor que el grado del denominador. Por ello lo primero es dividir los polinomios.
![]()
Sustituyendo en la integral:
![]()
Esta nueva integral la podemos resolver por la técnica de fracciones simples. Para ello hay que factorizar el denominador: (x4–1)=(x–1)(x+1)(x2+1). Podemos tratar de encontrar integrales del tipo racional y del tipo arcotangente. Por eso vamos a tratar de expresar el integrando como fracciones simples de la siguiente manera:
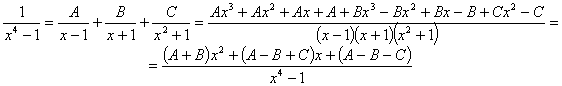
Comparando el numerador del quebrado inicial y el final planteamos el sistema:

por lo tanto:
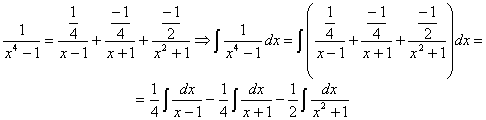
ahora tenemos dos integrales racionales inmediatas
utilizando la relación: ![]() y otra integral tipo
arcotangente, también inmediata utilizando la relación:
y otra integral tipo
arcotangente, también inmediata utilizando la relación: ![]()
![]()
87) ![]()
RESOLUCIÓN: Esta integral la podemos resolver por la técnica de fracciones simples. Para ello ya tenemos factorizado el denominador: (x–2)(x+2)(x2+10x+26). Vamos a tratar de expresar el integrando como fracciones simples teniendo en cuenta que uno de los polinomios es de segundo grado:
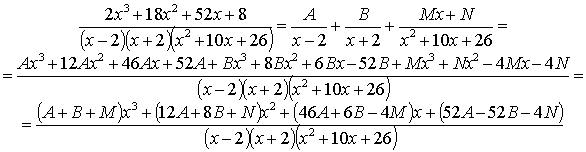
Comparando el
numerador del quebrado inicial y el final planteamos el sistema:

por lo tanto:

Ahora tenemos que resolver la integral racional, que es del tipo arcotangente. Esto se puede ver cuadrando el denominador:
![]()
Sustituyendo queda:
![]()
88) ![]()
RESOLUCIÓN: Vamos a tratar de convertir esta integral en una del
tipo potencial para poder resolverla utilizando la regla de integración ![]() . Para ello vamos a utilizar la relación fundamental de la
trigonometría:
. Para ello vamos a utilizar la relación fundamental de la
trigonometría: ![]()
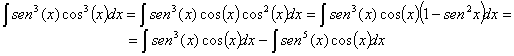
Hemos obtenido dos integrales
potenciales inmediatas que podemos resolver con la relación de integración ![]() de la siguiente
manera:
de la siguiente
manera:
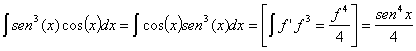
y
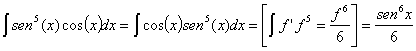
Estas integrales también pueden resolverse haciendo un cambio el variable t igual a la función:
![]()
y
![]()
sustituyendo los resultados tenemos resuelta la integral:
![]()
89) ![]()
RESOLUCIÓN: Vamos a tratar de convertir esta integral en una del
tipo potencial para poder resolverla utilizando la regla de integración ![]() . Para ello vamos a utilizar la relación fundamental de la
trigonometría:
. Para ello vamos a utilizar la relación fundamental de la
trigonometría: ![]()
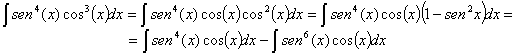
Hemos obtenido dos integrales
potenciales inmediatas que podemos resolver con la relación de integración ![]() de la siguiente
manera:
de la siguiente
manera:
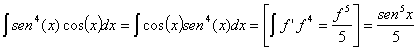
y
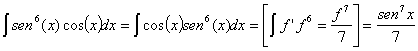
Estas integrales también pueden resolverse haciendo un cambio el variable t igual a la función:
![]()
y
![]()
sustituyendo los resultados tenemos resuelta la integral:
![]()
90) ![]()
RESOLUCIÓN: Vamos a tratar de convertir esta integral en una del
tipo potencial para poder resolverla utilizando la regla de integración ![]() . Para ello vamos a utilizar la relación fundamental de la
trigonometría:
. Para ello vamos a utilizar la relación fundamental de la
trigonometría: ![]()
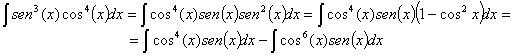
Hemos obtenido dos integrales
potenciales casi inmediatas (basta con multiplicar por –1 para tener la derivada
de la base) que podemos resolver con la relación de integración ![]() de la siguiente
manera:
de la siguiente
manera:
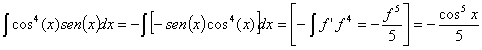
y

Estas integrales también pueden resolverse haciendo un cambio el variable t igual a la función:
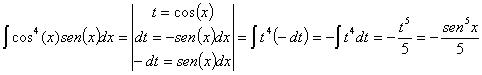
y
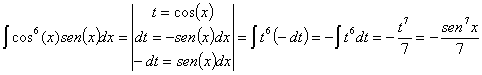
sustituyendo los resultados tenemos resuelta la integral:
![]()
91) ![]()
RESOLUCIÓN: Dado que integrar un producto es complicado, vamos a
tratar de convertirlo en una suma (o resta). Para ello utilizamos las
relaciones trigonométricas que convierten productos de senos por cosenos en
sumas: ![]()
![]()
92) ![]()
RESOLUCIÓN: Dado que integrar un producto es complicado, vamos a
tratar de convertirlo en una suma (o resta). Para ello utilizamos las
relaciones trigonométricas que convierten productos de senos por cosenos en
sumas: ![]()
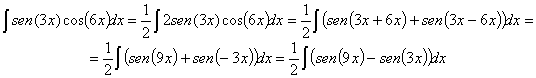
Hemos utilizado la propiedad del seno del ángulo opuesto: ![]()
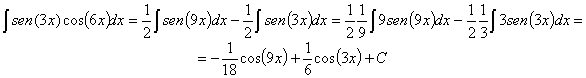
93) ![]()
RESOLUCIÓN: Dado que integrar un producto es complicado, vamos a
tratar de convertirlo en una suma (o resta). Para ello utilizamos las
relaciones trigonométricas que convierten productos de senos por senos en
sumas: ![]()
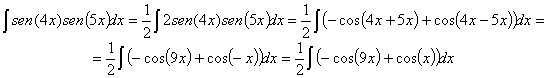
Hemos utilizado la propiedad del coseno del ángulo opuesto: ![]()

94) ![]()
RESOLUCIÓN: Dado que integrar un producto es complicado, vamos a
tratar de convertirlo en una suma (o resta). Para ello utilizamos las
relaciones trigonométricas que convierten productos de cosenos por cosenos en
sumas: ![]()
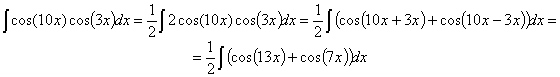
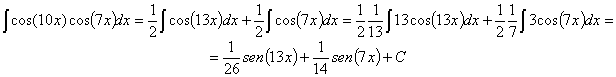
95) ![]()
RESOLUCIÓN: En este tipo de integrales vamos a utilizar uno de los cambios de variables “mágicos”, que es:
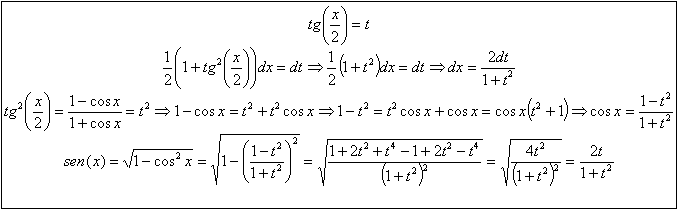
Vamos a sustituir las expresiones del seno y coseno halladas:

Hemos conseguido una integral racional inmediata utilizando
la regla de integración: ![]()
![]()
96) ![]()
RESOLUCIÓN: Vamos
a utilizar la ley fundamental de la trigonometría: ![]()
![]()
Ahora tenemos dos integrales que son inmediatas (la segunda es obvio). Veamos la primera de ellas:
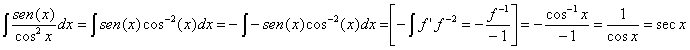 Ahora sustituimos en la integral:
Ahora sustituimos en la integral:
![]()
97) ![]()
RESOLUCIÓN: Multiplicamos y dividimos por cos(x):
![]()
Vamos a hacer el cambio de variable t=sen(x)
![]()
Esta integral es una racional que se podrá resolver por partes, pero primero hay que dividir los polinomios ya que el grado del numerador es mayor que el del denominador:
![]()
sustituyendo en la integral:
![]()
La última integral podemos resolverla por fracciones simples. Para ello factorizamos el denominador así:1-t2=(1+t)(1-t), y expresamos el quebrado de la siguiente manera:
![]()
Comparando los numeradores planteamos el sistema:
![]()
Queda:
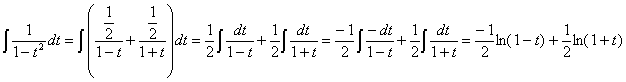
Vamos a sustituir en la integral anterior:
![]()
y a deshacer el cambio t=sen(x)
![]()
98) ![]()
RESOLUCIÓN: Vamos
a utilizar la fórmula del coseno del ángulo mitad: ![]() . Utilizando esta relación podemos poner que:
. Utilizando esta relación podemos poner que: ![]()

La integral de la secante al cuadrado es inmediata.
99) ![]()
RESOLUCIÓN: Esta integral se puede convertir en la integral anterior manipulando el quebrado:
![]()
Para
resolver ![]() repasar el ejercicio
98.
repasar el ejercicio
98.
100) ![]()
RESOLUCIÓN: En este tipo de integrales vamos a utilizar uno de los cambios de variables “mágicos”, que es:
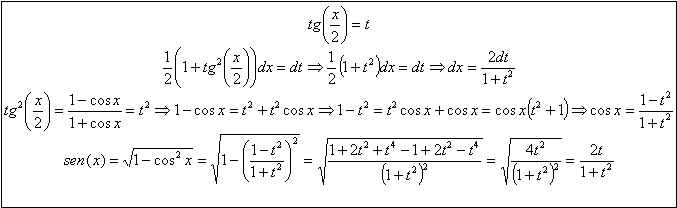
Vamos a sustituir las expresiones del seno y coseno halladas:

Esta nueva integral se puede resolver por fracciones simples factorizando: t2-3t+2=(t–1)(t–2)
![]()
Comparando los numeradores planteamos el sistema:
![]()
queda:
![]()
Sustituimos en la integral original y deshacemos el cambio de variable t=tg(x/2):
![]()