No hay caminos para la paz. La Paz es el camino Bienvenid@ a mi web

TALLER DE MATEMÁTICAS ASISTIDO POR ORDENADOR - 4º E.S.O.

Actividades propuestas:

Números naturales y números pares

Cuestiones:
  • Contar sin contar: ¿cómo sabrías si en una manifestación hay más chicos o hay más chicas? Recuerda, está prohibido contar... porque no hace falta.
  • ¿Hay más números pares que naturales? ¿es al revés? ¿por qué?
Puedes contestar aquí

El Hotel de Hilbert

Si un hotel está completo y viene alguién pidiendo una habitación no tendremos más remedio que decirle que no hay sitio. Sin embargo el Hotel de Hilbert es un tanto especial: tiene infinitas habitaciones. Podemos imaginarlo como un pasillo infinito con infinitas puertas numeradas (las habitaciones son unipersonales).
Cuestiones:
  • Si el hotel de Hilbert está completo y viene alguién pidiendo una habitación ¿se la podemos dar? ¿qué habitación le damos?
  • Si el hotel de Hilbert está completo y vienen 10 personas pidiendo habitación ¿qué habitación les damos?
  • Si llega el autocar infinito de Hilbert con infinitos pasajeros para alojarse en el Hotel de Hilbert, ¿cómo les alojamos? ¿qué habitaciones les damos?
Puedes contestar aquí

Sucesiones y series

Al contrario de lo que nos indica la intuición, sumando infinitos números no obtenemos siempre infinito.
Cuestiones:
  • ¿Cuánto da la siguiente suma infinita? 1 + 2 + 3 + 4 + 5 +... (pon la suma en notación sumatorio)
  • ¿Cuánto da la siguiente suma infinita: 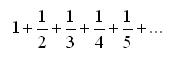serie armónica conocida como serie armónica?
  • ¿Cuánto da la siguiente suma infinita 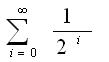serie de los inversos de las potencias de dos (serie de los inversos de las potencias de dos)?
  • ¿Cuánto da la siguiente suma infinita 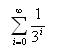serie de los inversos de las potencias de tres (serie de los inversos de las potencias de tres)?
Puedes contestar aquí
Propuesta de Adrián Tamayo:

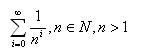
¿Cuánto vale la suma infinita serie de los inversos de las potencias de tres (serie de los inversos de las potencias de n) para n natural mayor que 1?
Puedes contestar aquí

¿Números imposibles?

Hay números que NO SE PUEDEN EXPRESAR COMO UN QUEBRADO... ¿cuáles son estos números? ¿Puedes decir alguno?
Pistas:
  • Escribe unos cuantos quebrados variados y calcula su valor (usa una calculadora si quieres... pero ten cuidado). Observa cómo son los decimales que salen
  • ¿Hay decimales que no pueden salir de dividir un quebrado? ¿cuáles son?
  • Di cuáles de las siguientes fracciones son siempre reducibles: Par/Par, Par/Impar, Impar/Par, Impar/Impar
Puedes contestar aquí

Sumando divisores: la función sigma de Euler

La función sigma de un número entero N se calcula sumando TODOS los divisores de ese número.
Por ejemplo, si queremos calcular 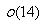debemos primero hallar los divisores de 14, que son 1, 2, 7 y 14.
Entoces la función sigma de 14 será:

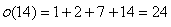
Cuestiones:

  1. Calcula las funciones sigma desde 1 hasta 13
  2. ¿Cómo son las funciones sigma de los números primos? ¿cuánto valen? Según esto ¿el 1 es primo?
  3. Halla el valor de la función sigma de las potencias de 2.¿Cuánto vale ?
Puedes contestar aquí

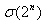Seguimos sumando divisores...

Para ver qué es la función sigma de Euler mira el apartado anterior... y practica, ¡porque ahora hay nuevos retos!
Cuestiones:

  1. ¿Cuánto valdrá la función sigma del producto de dos números?
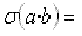
  2. Si ya has contestado al enigma anterior... prueba con este:
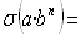
  3. Después del tanto entrenamiento esta cuestión es fácil:
Puedes contestar aquí

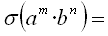
Lugares geométricos: la circunferencia

Un lugar geométrico está formado por un conjunto de puntos que cumplen una determinada propiedad.
Cuestiones:

  1. Halla la ecuación del lugar geométrico del conjunto de puntos que equidistan 5 unidades de otro punto C, de coordenadas (0,0)
  2. Halla la ecuación del lugar geométrico del conjunto de puntos que equidistan R de un punto C(cx, cy)
Puedes contestar aquí

Representando rectas

Las funciones de la forma f(x) = m·x + n tienen como gráfica una recta.
Cuestiones:

  1. ¿Qué significado geométrico tiene el parámetro n?
  2. ¿Qué significado geométrico tiene el parámetro m?
Puedes contestar aquí

Parábolas

Cuestiones:

  1. ¿Cómo puedes determinar el vértice de una parábola? Recuerda, buscaremos cuadrados perfectos aunque no los haya...
  2. ¿Cómo son todas las parábolas que tienen el mismo parámetro a?
Puedes encontrar aquí cómo encontrar cuadrados perfectos (reales o corregidos) y su relación con la ecuación de segundo grado.
Puedes contestar aquí

Estudiando funciones

Recuerda:

  1. En el estudio del dominio nos deben preocupar los denominadores y las raíces (si existen).
  2. Los puntos excluidos del dominio suelen estar relacionados con las asíntotas verticales.
  3. La asíntota horizontal puedes determinarla viendo qué ocurre si la x se hace infinito (positivo y negativo)
  4. El corte con el eje X se determina igualando la función a cero
  5. El corte con el eje Y se determina igualando x a cero
  6. Estudiar el signo de la función es igual que analizar la inecuación
Puedes contestar aquí
dmdelrio©2007