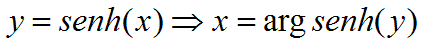FUNCIONES HIPERBÓLICAS
Se llaman así a las funciones:
Existen muchas analogías entre estas funciones y las correspondientes
funiones trigonométricas. Lo mejor es verlo gráficamente:

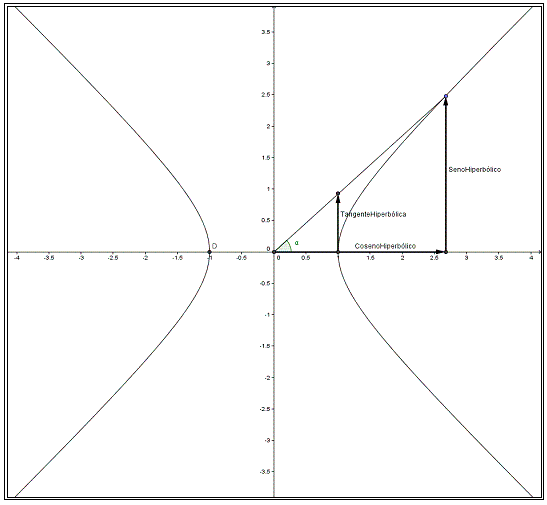
Las líneas trigonométricas se definen sobre la
circunferencia de radio unidad (x2 + y2
= 1) y las hiperbólicas sobre la hipérbola fundamental
(x2 - y2 = 1)
Las líneas hiperbólicas se relacionan entre sí
con expresiones parecidas a las que relacionan las líneas
trigonométricas: cosh2x - senh2x
= 1, que se puede demostrar fácilmente utilizando las definiciones
de las funciones hiperbólicas:
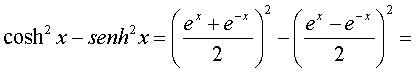
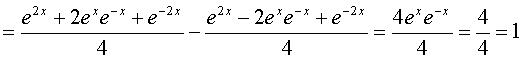
De la misma forma podemos determinar las expresiones de las derivadas
del seno y coseno hiperbólico de f:
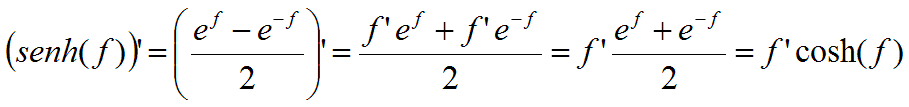
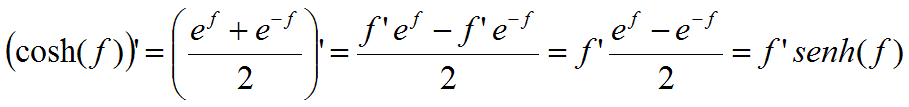
Ejercicio.- Puedes tratar de encontrar la expresión
para la derivada de la tangente hiperbólica de f(x).
La forma de las funciones hiperbólicas es:
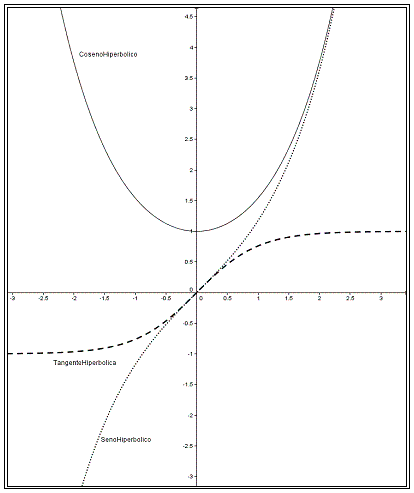
Las funciones hiperbólicas también tienen funciones
recíprocas. Se llama argumento al ángulo
sobre el que actúa la función. Por lo tanto, la
recíproca de la función seno hiperbólico
es la función argumento del seno hiperbólico, etc.